-
13. 선형 변환 (Linear Transformation)practice_선형대수 2024. 10. 4. 11:30
Q. 선형대수에서 선형 변환(Linear Transformation)의 정의는 무엇인가요.
A.
*선형 변환(linear transformation)**은 벡터 공간에서 한 벡터를 다른 벡터로 변환하는 함수로, 이 함수는 두 가지 중요한 속성을 만족합니다:

반시계방향, 시계방향변경가능

다양한 변환을 나타날수있음




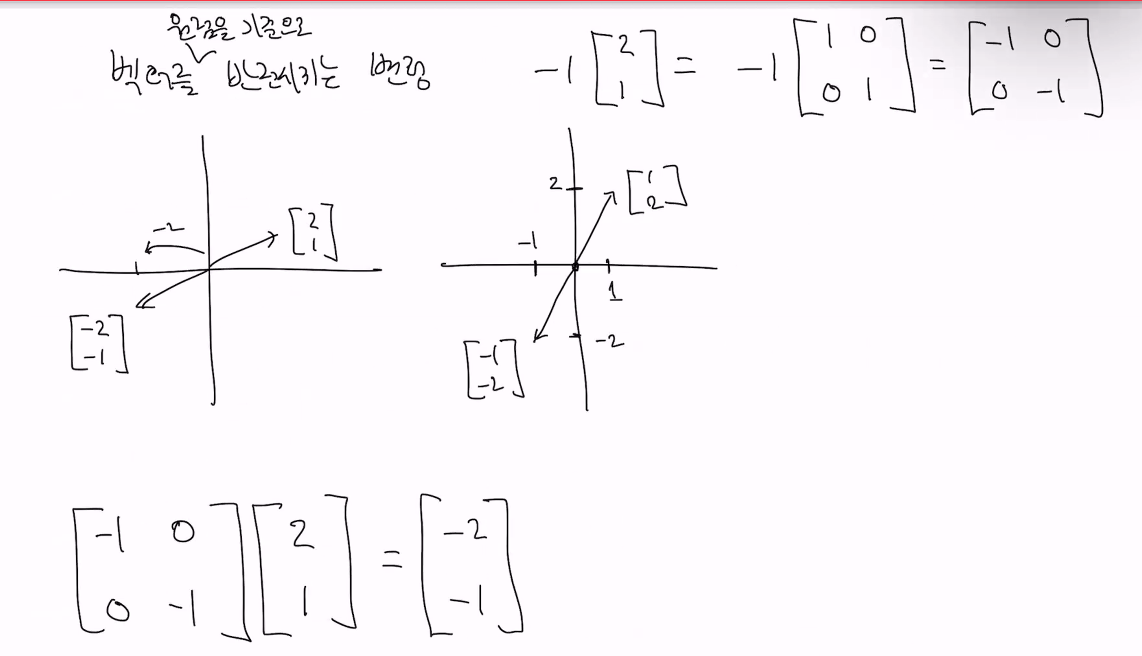
벡터회전
 •선형 변환은 이와 같이, 주어진 벡터를 다양하게 변형시키는 것이다•모든 선형 변환은 행렬로 나타낼 수 있다•일반적인 예시는 다음과 같다 (다른 선형 변환도 있음)•길이 늘이기 / 줄이기•회전시키기•반전시키기•또한 이러한 선형 변환 (행렬)등을 곱해서 하나로 합칠 수 있다
•선형 변환은 이와 같이, 주어진 벡터를 다양하게 변형시키는 것이다•모든 선형 변환은 행렬로 나타낼 수 있다•일반적인 예시는 다음과 같다 (다른 선형 변환도 있음)•길이 늘이기 / 줄이기•회전시키기•반전시키기•또한 이러한 선형 변환 (행렬)등을 곱해서 하나로 합칠 수 있다------------------------------
** 아래그림)
•어떠한 2차원 벡터가 있다고 하자. •우리는 이 벡터를 (2차원 안에서) 다양한 방법으로 변환시킬 수 있다.•단순히 생각해봤을때, 이 벡터를 반전시킬수도 있고, 임의의 각도로 회전시킬수도 있다•비슷하게, 길이를 늘릴 수도 있고, 줄일 수도 있다
•우리는 이 벡터를 (2차원 안에서) 다양한 방법으로 변환시킬 수 있다.•단순히 생각해봤을때, 이 벡터를 반전시킬수도 있고, 임의의 각도로 회전시킬수도 있다•비슷하게, 길이를 늘릴 수도 있고, 줄일 수도 있다


** 아래그림)

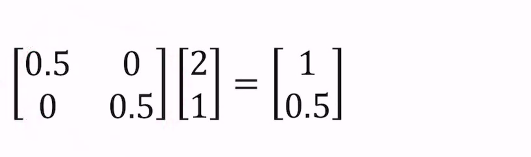 •이는 다른 2차원 벡터들에도 모두 동일하게 적용된다•만약 벡터를 원점기준으로 반전시키고 싶다면, 단위 행렬에 -1을 곱하면 된다2차원 벡터의 길이 변형을 행렬로 표현할 수 있다
•이는 다른 2차원 벡터들에도 모두 동일하게 적용된다•만약 벡터를 원점기준으로 반전시키고 싶다면, 단위 행렬에 -1을 곱하면 된다2차원 벡터의 길이 변형을 행렬로 표현할 수 있다

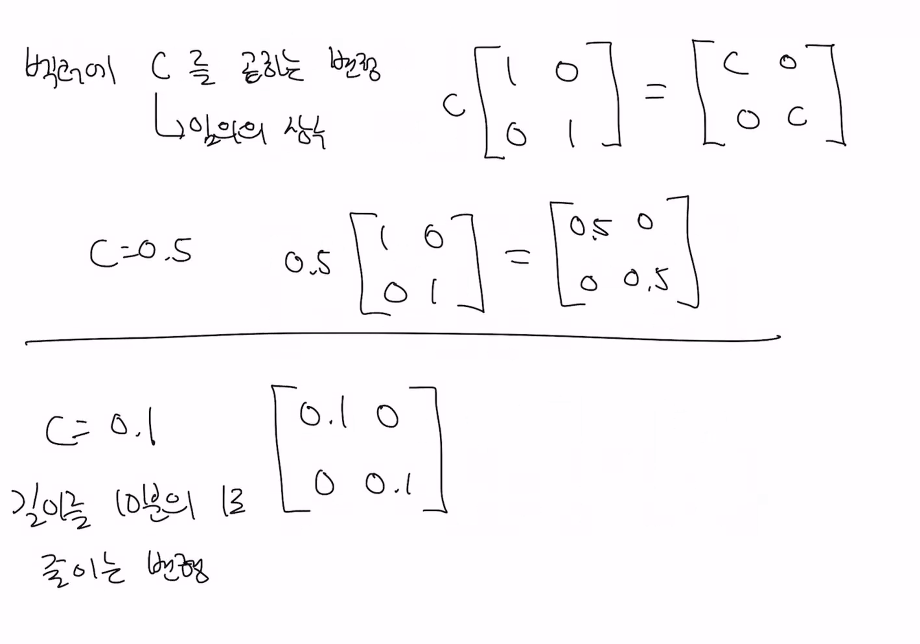
 여러변환을 하나로 합칠수있을까반으로 줄이는 행렬, 30도 회전시키는 행렬
여러변환을 하나로 합칠수있을까반으로 줄이는 행렬, 30도 회전시키는 행렬
'practice_선형대수' 카테고리의 다른 글
14. 중앙값(Median)과 평균(Mean)의 차이점과 각각의 장점 (0) 2024.10.04 03.2 확률 변수의 기댓값의 성질과 기댓값의 선형성(Linearity of Expectation) (0) 2024.10.04 12.다중 공선성 (Multicollinearity) (0) 2024.10.04 12-1 행렬의 랭크(Rank)의 정의와 중요성 (1) 2024.10.03 확률론에서 베이즈 정리(Bayes' Theorem)의 기본 개념과 활용 (0) 2024.10.01