12.다중 공선성 (Multicollinearity)

 

Q. 회귀 분석(에서 다중 공선성(Multicollinearity)의 개념과 이를 test방법은 무엇인가요

 

다중공선성: 독립변수들 사이에 큰 상관관계가 있다면 회귀분석이 불안정해짐

 

    1. 다중 공선성은 회귀 모델에서 독립 변수들 간에 높은 상관관계가 있는 상태를 의미합니다.

     2. 이는 회귀분석을 불안정하게 만들수 있다.

 

     3. 이것을 해결하려면, 상관 행렬을 통해 높은 상관관계를 가진 독립변수들을 찾아내고, 

        둘중 하나를 제거하거나, PCA를 통해 하나로 합칠수 있다.

 

 

•예를 들어서, 집의 크기, 위치, 방의 개수 등은 독립 변수고

•이를 통해서 집값 (종속 변수)를 예측하는 것입니다

 

집의 크기가 1평이 커질수록 집가격이 2천만원씩 커진다.

지하철역까지 거리는 1km 늘어날수록 집값 2천만원씩 하락

방의갯수 하나씩 증가할때마다 집값 5천만원 상승

회귀계수 -> 독립변수, 종속변수의 연관성찾음

 

 

회귀분석(Regression Analysis)은 변수들 간의 관계를 분석하고, 하나 이상의 독립 변수(설명 변수)가 종속 변수(목표 변수)에 어떻게 영향을 미치는지를 설명하거나 예측하는 통계 기법입니다. 주로 연속형 데이터의 예측을 위해 사용됩니다.

회귀분석에는 여러 종류가 있으며, 대표적인 유형은 다음과 같습니다:

회귀분석은 특히 머신러닝에서 중요한 기법 중 하나로, 데이터의 패턴을 모델링하여 예측하거나 설명하는 데 활용됩니다.

 

 

찾는방법:

독립변수들 사이의 상관계수를 다 조사한후 큰 상관계수들을 가진 독립변수들을 찾는다.

 

해결책 :

1. PCA를 사용해서 큰 상관관계가 있는 독립변수들을 작은차원으로 줄임(한두개로 합침) -> 새로운축이름 PCA1

2. 상관계수를 다 조사한후 큰 상관계수를 가진 독립변수를  둘중하나 제거

 

•회귀 분석은 독립 변수들을 사용해 종속 변수의 값을 예측하는 것입니다

 

•예를 들어서, 집의 크기, 위치, 방의 개수 등은 독립 변수고

•이를 통해서 집값 (종속 변수)를 예측하는 것입니다

 

집의 크기가 1평이 커질수록 집가격이 2천만원씩 커진다.

지하철역까지 거리는 1km 늘어날수록 집값 2천만원씩 하락

방의갯수 하나씩 증가할때마다 집값 5천만원 상승

회귀계수 -> 독립변수, 종속변수의 연관성찾음

 

독립변수들 사이에 큰 상관관계가 있다면,(다중공선성) (예, 집크기: 평<-> 제곱미터)

회귀계수의 추정(계산)이 불안정해진다. 0으로 나올수 있어서.

-> 사람이 확인할때 회귀계수가 0으로 나오면 상관없는거로 판단할수 있어서

 

PCA를 사용해서 큰 상관관계가 있는 독립변수들을 작은차원으로 줄임(한두개로 합침) -> 새로운축이름 PCA1

 

 

 

Multi  col  linearity

 

다중    변수  선형관계(상관관계)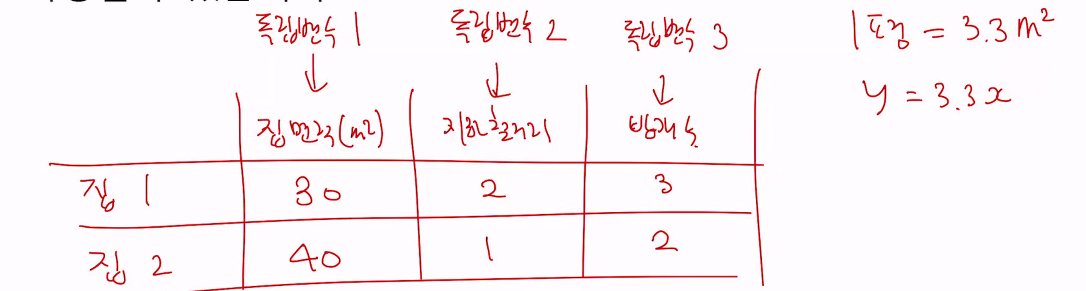

 

 

A. 1. 다중 공선성은 회귀 모델에서 독립 변수들 간에 높은 상관관계가 있는 상태를 의미합니다.

     2. 이는 회귀분석을 불안정하게 만들수 있다.

 

     3. 이것을 해결하려면, 상관 행렬을 통해 높은 상관관계를 가진 독립변수들을 찾아내고, 

        둘중 하나를 제거하거나, PCA를 통해 하나로 합칠수 있다.

 

 

•회귀 분석은 독립 변수들을 사용해 종속 변수의 값을 예측하는 것입니다

•예를 들어서, 집의 크기, 위치, 방의 개수 등은 독립 변수고

•이를 통해서 집값 (종속 변수)를 예측하는 것입니다

•이때 회귀 분석 모델은 독립 변수들이, 말 그대로 서로 독립적이라고 가정합니다.

•회귀 분석 모델은 각각의 독립 변수들이 종속 변수에 미치는 영향을 계산합니다.

•이러한 영향은 회귀 계수로 나타납니다.

 

** 아래그림)

•하지만 두 독립 변수를 같이 사용하면 문제가 발생합니다.

•회귀 모델은 집 크기 (제곱미터) 만으로 이미 집값을 완벽하게 예측할 수 있습니다 (회귀 계수 백만)

•따라서, 모델에게 집크기 (평)은 무의미하고, 따라서 회귀 계수를 0으로 설정할 가능성이 있습니다.

•이는 비 정상적인 회귀 계수입니다

 

 

** 아래그림)

 

상관계수행렬- 각 독립 변수들 사이의 상관 계수를 한번에 적은 것

독립변수들사이의 높은 상관계수가 있으면 이둘은 서로 독립이 아님 (서로 큰 영향을 주고받는다) 예, 집값 평 집값 m2

서로 큰 상관관계가 있는 독립변수들을 회귀분석에 사용하게되면, 회귀분석이 불안정해진다(비정상적인 회귀계수가 발생)

이를 해결하기 위해,

독립변수 1     이둘이 상관계수 0.9로 높은 상관관계가 있으면

독립변수 2

해결책

1) 하나를 제거한다.

2) PCA를 써서 하나로 합친다.

 

 

 

 

회귀분석(Regression Analysis)은 변수들 간의 관계를 분석하고, 하나 이상의 독립 변수(설명 변수)가 종속 변수(목표 변수)에 어떻게 영향을 미치는지를 설명하거나 예측하는 통계 기법입니다. 주로 연속형 데이터의 예측을 위해 사용됩니다.

회귀분석에는 여러 종류가 있으며, 대표적인 유형은 다음과 같습니다: