확률론에서 베이즈 정리(Bayes' Theorem)의 기본 개념과 활용

Q. 확률론에서 베이즈 정리(Bayes' Theorem)의 기본 개념과 활용 예시에 대해 설 명해 주세요.

 

•주어진 사건의 조건 하에서 다른 사건의 확률을 계산하는 데 사용됩니다.

•여러가지 용도가 있지만, 일반적으로 P(A|B)를 통해 P(B|A)를 추정할때 사용한다

전제조건이 P(A), P(B)를 알아야된다.

 

 

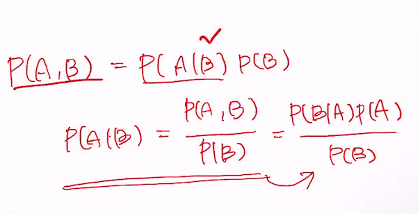
아래그림) P(A|B) = P(A given B) = B가 주어진 조건에 A를 구하는 확률

아래그림) 주사위 3이 나오면서 홀구인것은 1/6

 

•일반적으로, P(A|B)와 P(B|A)는 같지 않다  -> 다른거로 바꾸기 위해 사용한다.

 

 

•예시

•코로나 검사 키트가 있다. 만약 실제 코로나에 걸린 사람이 이 키트를 사용하면, 90%의 확률로 양성이 나온다.

•만약 어떤 사람이 이 검사를 해서 양성이 나왔다면, 이 사람이 90%의 확률로 코로나에 걸려 있다고 할 수 있을까?

 

아래그림

•코로나 검사 키트는 실제로 코로나에 걸린 사람이 검사를 했을때 90%의 확률로 양성 판정을 내린다

P(검사 양성 | 실제 코로나)  => 90%

•이때 우리가 알고 싶은 것은, 검사 양성이 나왔을 때 이 사람이 실제 코로나에 걸려 있을 확률이다

P(실제 코로나 | 검사 양성) => ?

•P(검사 양성 | 실제 코로나) 는 이미 0.9 (90%) 로 알려져 있다

•하지만 이를 통해 실제로 P(실제 코로나 | 검사 양성)을 계산하려면, 추가로 P(실제 코로나) 와 P(검사 양성) 의 확률들이 필요

만약 우리가 이 확률들을 알고 있다면 계산할 수 있다

 

•P(실제 코로나)는 코로나의 유병률이다

•만약 우리가 (다른 경로를 통해) 전체 인구 중 대략 1%가 코로나에 걸려있다는 것을 알게 되었다면, P(실제 코로나)는 1%이다.

•P(검사 양성)은 두가지로 구성되어 있다

•첫번째는 실제로 코로나를 가지고 있는 사람이 양성으로 판정될 확률

•두번째는 코로나에 걸리지 않았지만 양성으로 판정될 확률

•이 둘을 더하면 P(검사 양성)을 구할 수 있다

 

•이에 추가로, 코로나에 안 걸린 사람이 검사에서 양성으로 나올 확률을 10%라고 하자

•결과적으로, P(검사 양성) = (90% × 1%) + (10% × 99%) = 10.8%

 

아래그림

 

결론

만약 코로나에 안 걸렸는데 양성으로 (오진)할 확률을 현재 10%에서 1%로 줄인다면(보라색 아닌 파란부분)

현재의 90%에서 99%로 증가시키면, P(실제 코로나 | 검사 양성)이 47.6%로 크게 향상된다