벨만-포드(Bellman-Ford) 알고리즘과 다익스트라(Dijkstra) 알고리즘의 차이점과 사용

벨만-포드(Bellman-Ford) 알고리즘과 다익스트라(Dijkstra) 알고리즘의 차이점과 사용은 어떻게 사용되는지 알려주세요

 

•다익스트라와 벨만 포드 알고리즘은 모두 그래프에서 최단 경로를 구하기 위해 사용되는 알고리즘

 

•다익스트라는 보다 효율적인 대신, 양수 가중치만을 지원하고

벨만 포드는 상대적으로 비효율적이지만 음수 가중치도 사용 가능

 

아래그림)  다익스트라 알고리즘

 

 

 

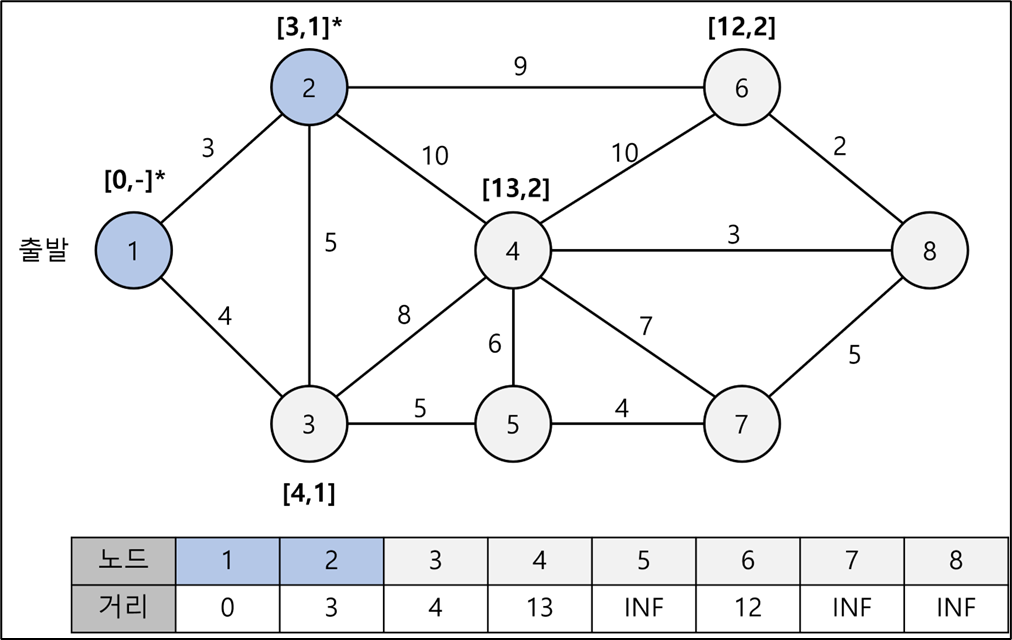
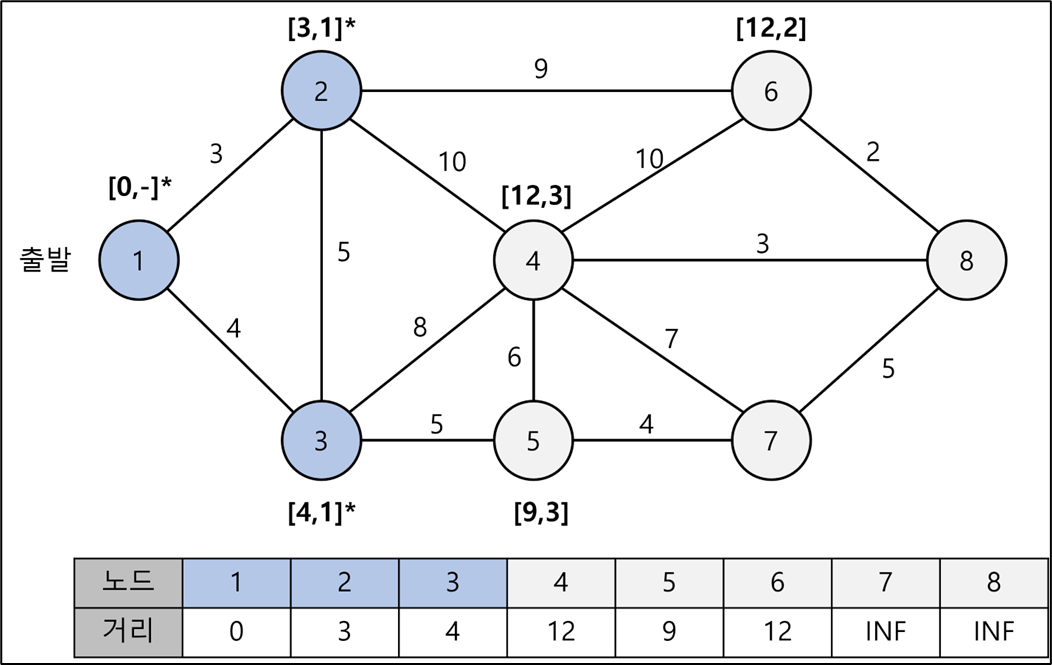
아래그림) 

•다익스트라 알고리즘은 각 단계에서 Greedy 하게, 가장 짧은 경로를 선택함

매 단계에서, 방문하지 않았던 노드 중에서, 가장 짧은 경로 선택

아래 예시에서 (1번에서 시작), 다익스트라는 1 -> 3을 선택할 것

 

 

아래그림_ 벨만-포드(Bellman-Ford) 알고리즘

출처 https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/

 

 

 

**벨만-포드(Bellman-Ford) 알고리즘**과 **다익스트라(Dijkstra) 알고리즘**은 둘 다 그래프에서 **최단 경로**를 찾는 알고리즘이지만, **동작 방식**과 **적용 가능한 상황**에서 차이가 있습니다. 각 알고리즘의 차이점과 사용 시점을 설명하겠습니다.

### 1. **알고리즘의 목적**

- **벨만-포드 알고리즘**: **음수 가중치**를 포함한 그래프에서도 **최단 경로**를 찾을 수 있는 알고리즘입니다. 음수 사이클(노드들이 반복적으로 순환하며 거리가 무한히 작아지는 경우)이 존재할 때는 이를 감지할 수 있습니다.
  
- **다익스트라 알고리즘**: **양수 가중치**만 있는 그래프에서 최단 경로를 찾는 데 매우 효율적인 알고리즘입니다. 음수 가중치가 있는 경우 올바른 결과를 보장하지 못합니다.

### 2. **시간 복잡도**

- **벨만-포드 알고리즘**: 시간 복잡도는 \(O(V \times E)\)로, 여기서 \(V\)는 노드의 수, \(E\)는 간선의 수입니다. 모든 간선을 \(V-1\)번 반복해서 확인하는 방식으로 동작합니다. 이 때문에 벨만-포드는 큰 그래프에 대해 상대적으로 비효율적입니다.
  
- **다익스트라 알고리즘**: 시간 복잡도는 **우선순위 큐**(힙 자료구조)를 사용하면 \(O((V + E) \log V)\)입니다. 이 방식은 벨만-포드보다 훨씬 효율적이며, 특히 **밀집 그래프**에서 빠른 성능을 발휘합니다.

### 3. **음수 가중치 처리**

- **벨만-포드 알고리즘**: **음수 가중치**를 가진 간선이 있는 그래프에서도 정확한 최단 경로를 찾을 수 있으며, **음수 사이클**이 존재하는지 여부도 감지할 수 있습니다.
  
- **다익스트라 알고리즘**: **음수 가중치**를 지원하지 않습니다. 음수 간선이 있으면 잘못된 경로를 탐색하게 되어 최단 경로를 찾을 수 없습니다.

### 4. **작동 방식**

- **벨만-포드 알고리즘**: 동적 프로그래밍 방식으로 동작하며, 모든 간선을 반복적으로 확인해 최단 경로를 업데이트합니다. 이는 그래프의 각 노드에 대해 최단 경로가 계속해서 개선될 수 있도록 하는 방식입니다.
  
- **다익스트라 알고리즘**: **탐욕적(greedy)** 방식으로 동작합니다. 출발 노드에서 가까운 노드부터 탐색하며, 이미 최단 경로가 확정된 노드에 대해서는 다시 계산하지 않습니다. 이 방식은 음수 간선이 없다는 가정 하에서 효율적으로 작동합니다.

### 5. **적용 가능한 그래프의 유형**

- **벨만-포드 알고리즘**:
  - **음수 가중치**가 있는 그래프에 적용 가능
  - 음수 가중치가 있는 경우나 음수 사이클을 감지해야 하는 경우 유용
  - 시간 복잡도가 크므로 작은 그래프에서 주로 사용

- **다익스트라 알고리즘**:
  - **양수 가중치**만 있는 그래프에서 매우 효율적
  - 대규모 그래프에서 사용 가능
  - 도로 네트워크, 통신망 등에서 자주 사용

### 6. **음수 사이클 감지**

- **벨만-포드 알고리즘**: **음수 사이클**이 있는지 확인할 수 있습니다. 알고리즘을 수행한 후에도 최단 경로가 더 작아질 수 있으면 음수 사이클이 존재하는 것입니다.
  
- **다익스트라 알고리즘**: 음수 사이클을 감지할 수 없으며, 음수 사이클이 존재하는 그래프에서는 잘못된 결과를 반환할 수 있습니다.

### 7. **알고리즘 사용 예**

- **벨만-포드 알고리즘 사용 사례**:
  - **금융 네트워크**: 음수 가중치(예: 금융 거래에서 손실 등)를 포함하는 시스템에서 최단 경로를 찾을 때 사용
  - **그래프에서 음수 사이클을 감지**해야 할 때
  - 일반적으로 그래프 크기가 상대적으로 작은 경우

- **다익스트라 알고리즘 사용 사례**:
  - **도로 네트워크**: 모든 경로의 가중치가 양수인 상황에서 최단 경로 탐색 (예: 네비게이션 시스템)
  - **인터넷 라우팅**: 데이터 패킷을 가장 빠른 경로로 전달하는 데 사용
  - **대규모 네트워크**에서 최단 경로 탐색

### 요약

 

### 결론

- **벨만-포드**는 **음수 가중치**나 **음수 사이클**을 다루어야 하는 상황에서 유용하며, 시간 복잡도가 높아 작은 그래프에 적합합니다.
- **다익스트라**는 **양수 가중치**만 있을 때 매우 효율적으로 동작하며, 큰 규모의 그래프에서도 빠르게 최단 경로를 찾을 수 있는 알고리즘입니다.