-
출처: 딥러닝·인공지능 Signature 초격차 패키지 Online.
•현재 a, b 위치에서 L을 줄이는 방향으로 나아가자•Gradient는 항상 가장 가파른 방향을 향한다..! (x2 으로 확인)왜 가장 가파른 방향? proof) 1-3강.
•그럼 그냥 반대 방향으로 가면 되겠네!그라디언트 - 편미분을 벡터로 쌓은것 - 그라디언트는 항상 가파른 방향으로 향한다.그래서 반대방향으로 가야 loss가 적어진다.오른쪽 벡터로 편미분값을 묶은것이 yx^2의 그라디언트x가 1일때 미분한값은 2x니까
2니까 x가 1일때 가장가파른 방향이니
반대방향은 -2
1과 -1을 계속 왔다갔다함 - > 그라디언트 크기를 고려를 안해준것임 -> 생각보다 미분값이 크다는겂
그래서 러닝 레이트를 곱해줌
x값이 1일때 x^2의 미분한값은 2x니까 2*1이니까 반대방향이니까 1-2
-1= 1-2 (x=1일때의 기울기의 반대방향)
1=-1+2(x=-1일때의 기울기의 반대방향)
경사하강법 알고리즘의 기본 흐름
- 초기화: 파라미터(예: 가중치, θ)를 임의의 값으로 설정.
- 반복: 다음의 과정을 비용 함수가 최소화될 때까지 반복:
- 비용 함수 J(θ)의 기울기 ∇J(θ)를 계산
- 파라미터를 업데이트:
- θ=θ−α∇J(θ)
- 여기서 α\alpha는 학습률(learning rate)이라고 하며, 한 번의 업데이트에서 파라미터를 얼마나 크게 변화시킬지 결정.
- 수렴: 기울기가 매우 작아지거나, 더 이상의 비용 감소가 일어나지 않을 때 알고리즘을 멈춤
결론 - 경사하강법
경사하강법(Gradient Descent)은 머신러닝과 최적화 문제에서 자주 사용되는 알고리즘 중 하나로, 목표는 비용 함수(또는 손실 함수)를 최소화하는 변수들의 최적 값을 찾는 것입니다. 경사하강법은 반복적으로 비용 함수의 기울기를 계산하고, 그 기울기의 반대 방향으로 이동함으로써 점차적으로 최적 해를 찾아가는 방식입니다.
### 경사하강법의 기본 개념
1. **목표**: 비용 함수를 최소화하는 파라미터(예: 가중치, 편향 등)를 찾는 것.
2. **기울기**: 특정 점에서 비용 함수의 기울기를 계산해, 그 방향이 비용을 증가시키는지 감소시키는지 확인.
3. **업데이트**: 기울기의 반대 방향으로 파라미터를 업데이트함으로써 점점 최소값에 가까워짐.
###경사하강법 알고리즘의 기본 흐름
- 초기화: 파라미터(예: 가중치, θ)를 임의의 값으로 설정.
- 반복: 다음의 과정을 비용 함수가 최소화될 때까지 반복:
- 비용 함수 J(θ)의 기울기 ∇J(θ)를 계산
- 파라미터를 업데이트:
- θ=θ−α∇J(θ)
- 여기서 α\alpha는 학습률(learning rate)이라고 하며, 한 번의 업데이트에서 파라미터를 얼마나 크게 변화시킬지 결정.
- 수렴: 기울기가 매우 작아지거나, 더 이상의 비용 감소가 일어나지 않을 때 알고리즘을 멈춤
### 경사하강법의 종류
1. **배치 경사하강법 (Batch Gradient Descent)**:
- 전체 데이터셋을 사용해 기울기를 계산.
- 모든 데이터에 대해 계산하기 때문에 정확하지만, 대규모 데이터셋에서는 계산 비용이 매우 큼.
2. **확률적 경사하강법 (Stochastic Gradient Descent, SGD)**:
- 하나의 샘플(데이터 포인트)에 대해 기울기를 계산하고 즉시 파라미터를 업데이트.
- 계산 비용이 적고 빠르게 수렴하지만, 파라미터가 항상 정확한 방향으로 움직이지 않기 때문에 비용 함수의 값이 불안정하게 변동할 수 있음.
3. **미니배치 경사하강법 (Mini-batch Gradient Descent)**:
- 데이터셋을 작은 배치로 나누어 각 배치에 대해 기울기를 계산하고 업데이트.
- 배치 경사하강법과 SGD의 장점을 결합한 방법으로, 계산 효율성과 수렴 속도 모두에서 이점을 가짐.
### 학습률(learning rate)의 중요성
- 학습률 \( \alpha \)는 경사하강법에서 매우 중요한 역할을 합니다.
- 너무 크면, 최소값을 지나쳐서 발산할 수 있음.
- 너무 작으면, 수렴 속도가 느려져 학습 시간이 길어짐.
### 경사하강법의 적용
경사하강법은 선형 회귀, 로지스틱 회귀, 신경망과 같은 머신러닝 알고리즘에서 주로 사용되며, 각 알고리즘의 손실 함수를 최소화하는 데 활용됩니다.
경사하강법에 대해 더 자세한 내용이나 관련 논문이 필요하면 추가로 검색해드릴 수 있습니다.
---
***Handling multiple papers?***
Our AI sidebar -- Sider assists you skim through papers 10X faster using its 10+ one-click research tools like deep reader, advanced search, ChatPDF, and context selection.
[Get ready for a smarter academic experience!](https://bit.ly/4aSnMXa)
2차원에서의 x가
3차원에서의 x, y이니까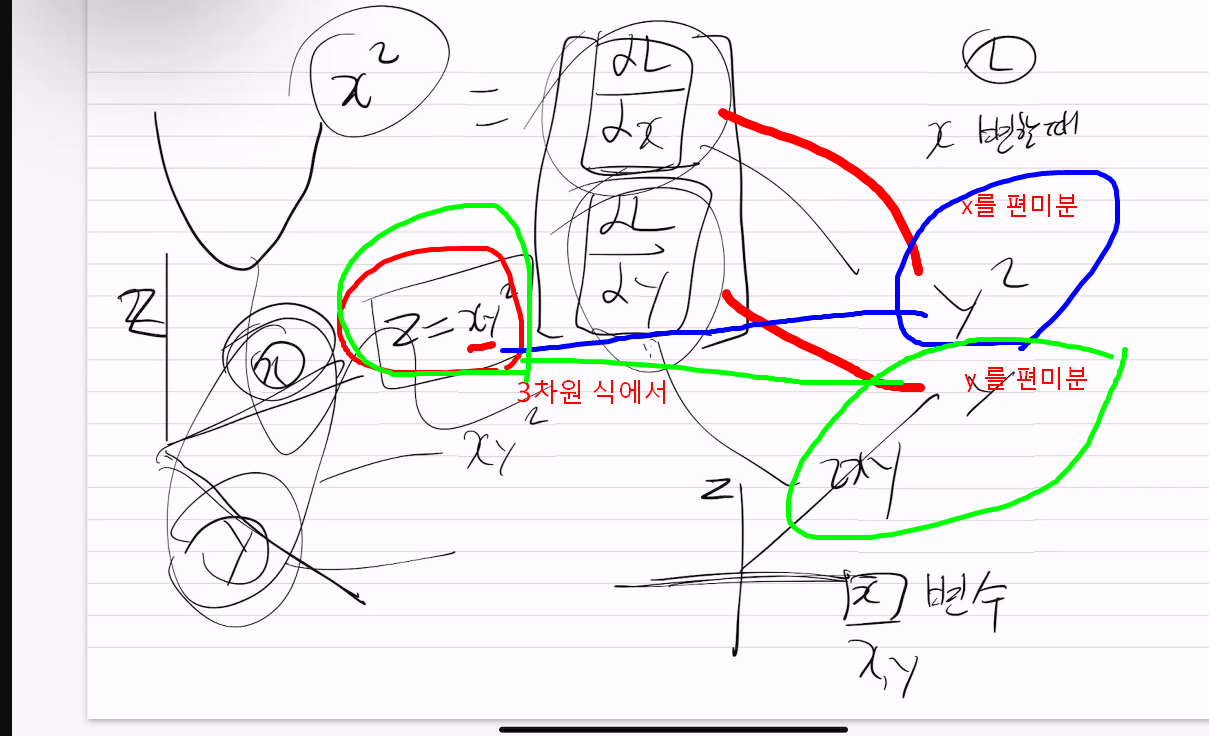
(4, 4)방향이 가장 가파르게 올려주는 방향 -> 그라디언트 : 가장 가파른 방향으로 향함
x를 기준으로 음수일때 x의 왼쪽이 그래프를 가장 가파르게,
x를 기준으로 양수일때 x의 오른쪽이 그래프를 가장
가파르게하는 x의방향
argmin 1/5 L = argmin L => L을 최소화하나 1/5을 최소화하나 a, b는 똑같아서 나누기 5(1/5) 안해도됨
a, b a, b
1/5L(1/5 의 loss) 최소값, L의최소값 의 a, b는 다름
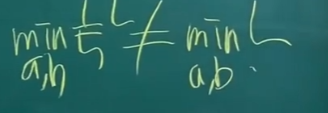
y x^2의 편미분
yx^2을 x로 편미분하면 2yx
yx^2을 y로 편미분하면 x^2
2yx -> 이 두개를 묶은것이 gradient
x^2
아래그림) yx^2의 그라디언트
= 도함수(곡선의 기울기)
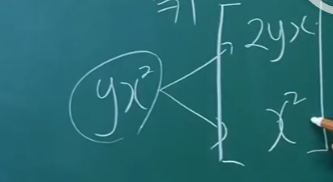
도함수
출처: chatgpt
도함수(derivative)는 미분(calculus)에서 중요한 개념으로, 함수가 특정한 점에서 얼마나 빠르게 변하는지를 나타냅니다. 즉, 도함수는 함수의 기울기(변화율)를 계산하는 수학적 도구입니다. 이를 통해 함수의 변화량을 분석하거나, 최댓값과 최솟값 같은 극값을 찾는 데 사용됩니다.
도함수의 정의
함수 f(x)f(x)의 도함수는 다음과 같이 정의됩니다:
f′(x)=limh→0f(x+h)−f(x)hf'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}이 식은 함수의 변화율을 정의하는데, 함수가 xx에서 아주 작은 값 hh만큼 변할 때 그 변화량을 계산한 것입니다. 이때 hh를 0으로 보내면 아주 미세한 변화에 대한 함수의 기울기를 구할 수 있습니다.
도함수의 의미
- 속도: 도함수는 물리학에서 속도나 가속도를 계산하는 데 활용됩니다. 예를 들어, 물체의 위치를 시간의 함수로 나타낸다면, 그 도함수는 물체의 속도를 의미합니다.
- 기울기: 도함수는 그래프에서 곡선의 기울기를 나타냅니다. 예를 들어, 함수의 그래프에서 특정 점에서의 기울기는 그 점에서의 순간적인 변화율을 나타냅니다.
도함수의 계산법
몇 가지 기본적인 도함수 규칙은 다음과 같습니다:
- 상수 함수 f(x)=cf(x) = c인 경우, f′(x)=0f'(x) = 0입니다.
- 거듭제곱 함수 f(x)=xnf(x) = x^n인 경우, f′(x)=n⋅xn−1f'(x) = n \cdot x^{n-1}입니다.
- 합의 미분: 두 함수의 합 f(x)+g(x)f(x) + g(x)의 도함수는 f′(x)+g′(x)f'(x) + g'(x)입니다.
- 곱의 미분: f(x)⋅g(x)f(x) \cdot g(x)의 도함수는 f′(x)⋅g(x)+f(x)⋅g′(x)f'(x) \cdot g(x) + f(x) \cdot g'(x)입니다.
- 연쇄 법칙: 복합 함수 f(g(x))f(g(x))의 도함수는 f′(g(x))⋅g′(x)f'(g(x)) \cdot g'(x)입니다.
예시
- 1차 함수: f(x)=3x+2f(x) = 3x + 2f′(x)=3f'(x) = 3(기울기가 일정한 직선이므로 도함수는 상수입니다.)
- 2차 함수: f(x)=x2f(x) = x^2f′(x)=2xf'(x) = 2x(이 함수의 기울기는 점에 따라 변합니다.)
도함수는 다양한 수학적, 과학적 응용에서 매우 중요하며, 함수의 특성과 변화를 이해하는 데 큰 역할을 합니다.