6.행렬 (단위행렬, 역행렬, 전치행렬)

Q. 선형대수에서 행렬의 역행렬(Inverse Matrix)의 개념과 계산 방법은 어떻게 될까요

A. 역행렬은 주어진 행렬과 곱했을 때 단위 행렬로 되는 행렬입니다.

 

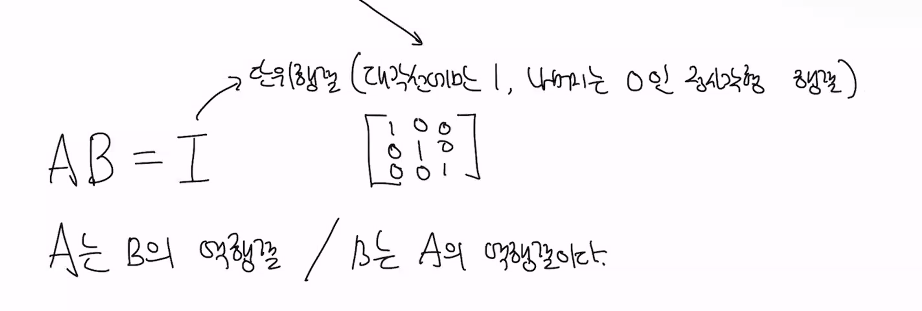
     역행렬을 계산하기 위해서는 주어진 행렬이 정방행렬이어야 하며, 주로 가우스-조르당 소거법 또는 수식적인 방법을 사용하여 계산합니다.

전치행렬 ( 행과 열을 뒤집는다 ) A-> AT

 

 

행렬이란?

•1개 이상의 수를 직사각형의 배열로 나열한 것

 

•한 개의 행만 가지는 행렬을 (1 x N) 행벡터로, 비슷하게 한 개의 열만 가지는 행렬을 (N x 1) 열벡터라고도 한다

 

•행렬 중에서 행과 열의 개수가 동일한 것들을 정방행렬 (Square matrix)라고 한다 (4x4, 3x3 등)

•또한, 정방행렬 중 대각선 (Diagonal)만 1이고, 나머지는 모두 0인 행렬을 단위행렬 (Identity matrix)라고 한다

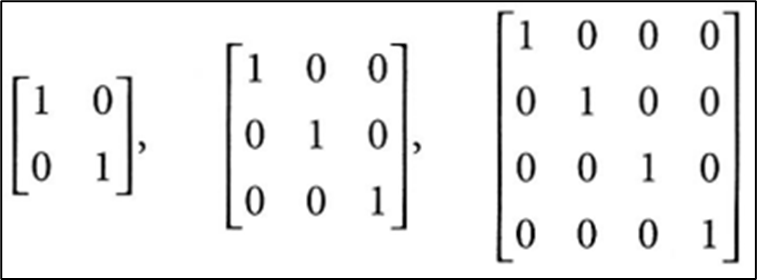
•임의의 정방행렬 A와, 같은 크기를 가진 단위행렬을 곱하면, 결과값은 A가 그대로 나온다

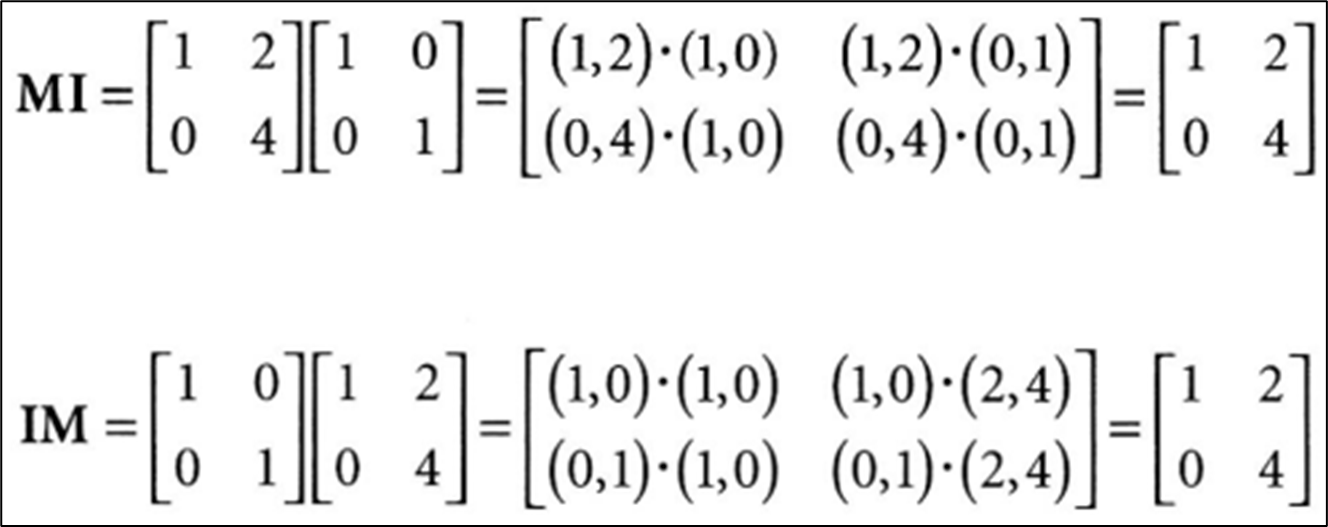
•만약 임의의 정방행렬 A와, 다른 정방행렬 B를 곱해서 단위행렬이 나온다면, B는 A의 역행렬이라고 한다

 

•AB = I (단위행렬)이면, A는 B의 역행렬이다

•반대로 B 또한 A의 역행렬이다

 

•실제로 역행렬을 계산하는 것은 매우 복잡하며 (손으로 계산하려면 3x3 부터 매우 복잡해짐), 일반적으로는 컴퓨터를 통해 수식적 방법으로 계산함